Batch Normalization – forward
Batch normalization is a really interesting technique that reduces internal covariate shift and accelerates the training of deep neural nets. Read the original paper for more details.
A word about notation
Batch normalization is applied across feature axis. For e.g. if we have a batch of three samples and each sample has five dimensions as follows
In batch normalization, the normalization is done across feature axis.
We can define the mean and variance across the features axis as follows
\[\begin{align} \mu_{k} = \frac{1}{3}\sum_{i=0}^{2} x_{i,k} \end{align}\] \[\begin{align}\label{eqn:sigma} \sigma_{k}^2 = \frac{1}{3}\sum_{i=0}^{2}(x_{i,k} - \mu_{k})^2 \end{align}\]and the batch normalized matrix will look as follows
\[\begin{align} \label{eqn:xhat} \hat{x} = \begin{pmatrix} \frac{x_{0,0} - \mu_{0}}{\sqrt{\sigma_{0}^2 + \epsilon}} & \frac{x_{0,1} - \mu_{1}}{\sqrt{\sigma_{1}^2 + \epsilon}} & \frac{x_{0,2} - \mu_{2}}{\sqrt{\sigma_{2}^2 + \epsilon}} & \frac{x_{0,3} - \mu_{3}}{\sqrt{\sigma_{3}^2 + \epsilon}} & \frac{x_{0,4} - \mu_{4}}{\sqrt{\sigma_{4}^2 + \epsilon}} \\ \frac{x_{1,0} - \mu_{0}}{\sqrt{\sigma_{0}^2 + \epsilon}} & \frac{x_{1,1} - \mu_{1}}{\sqrt{\sigma_{1}^2 + \epsilon}} & \frac{x_{1,2} - \mu_{2}}{\sqrt{\sigma_{2}^2 + \epsilon}} & \frac{x_{1,3} - \mu_{3}}{\sqrt{\sigma_{3}^2 + \epsilon}} & \frac{x_{1,4} - \mu_{4}}{\sqrt{\sigma_{4}^2 + \epsilon}} \\ \frac{x_{2,0} - \mu_{0}}{\sqrt{\sigma_{0}^2 + \epsilon}} & \frac{x_{2,1} - \mu_{1}}{\sqrt{\sigma_{1}^2 + \epsilon}} & \frac{x_{2,2} - \mu_{2}}{\sqrt{\sigma_{2}^2 + \epsilon}} & \frac{x_{2,3} - \mu_{3}}{\sqrt{\sigma_{3}^2 + \epsilon}} & \frac{x_{2,4} - \mu_{4}}{\sqrt{\sigma_{4}^2 + \epsilon}} \end{pmatrix} \end{align}\]Where \(\epsilon\) is a very small value added to the denominator to prevent division by zero. The normalized activation is scaled and shifted:
\[\begin{align}\label{eqn:bn} y = \gamma \hat{x} + \beta \end{align}\]where
\[\gamma = \begin{pmatrix} \gamma_0 & \gamma_1 & \gamma_2 & \gamma_3 & \gamma_4 \end{pmatrix}\]and
\[\beta = \begin{pmatrix} \beta_0 & \beta_1 & \beta_2 & \beta_3 & \beta_4 \end{pmatrix}\]The parameters \(\gamma\) and \(\beta\) are learned along with the original model parameters. They help restore the representational power of the network. This methodology can applied in python as follows:
def batchnorm_forward(x, gamma, beta, bn_param):
mode = bn_param['mode']
eps = bn_param.get('eps', 1e-5)
momentum = bn_param.get('momentum', 0.9)
N, D = x.shape
running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))
running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype))
out, cache = None, None
if mode == 'train':
sample_mean = x.mean(axis=0)
running_mean = momentum * running_mean + (1 - momentum) * sample_mean
sample_var = x.var(axis=0)
running_var = momentum * running_var + (1 - momentum) * sample_var
x_norm = (x - sample_mean)/np.sqrt(sample_var + eps)
out = gamma*x_norm + beta
cache = {}
cache['gamma'] = gamma
cache['beta'] = beta
cache['x_norm'] = x_norm
cache['x'] = x
cache['sample_mean'] = sample_mean
cache['sample_var'] = sample_var
cache['eps'] = eps
cache['N'], cache['D'] = N, D
elif mode == 'test':
x_norm = (x - running_mean) / np.sqrt(running_var + eps)
out = gamma * x_norm + beta
else:
raise ValueError('Invalid forward batchnorm mode "%s"' % mode)
# Store the updated running means back into bn_param
bn_param['running_mean'] = running_mean
bn_param['running_var'] = running_var
return out, cache
Batch Normalization – backward
Calculating batch normalization via the computation graph is quite tedious. Review the details of matrix multiplication bacward propogation in the lecture 4 handouts to better understand the derivation given below.
Lets start with the computation graph of the forward pass first and then go through the backward pass.
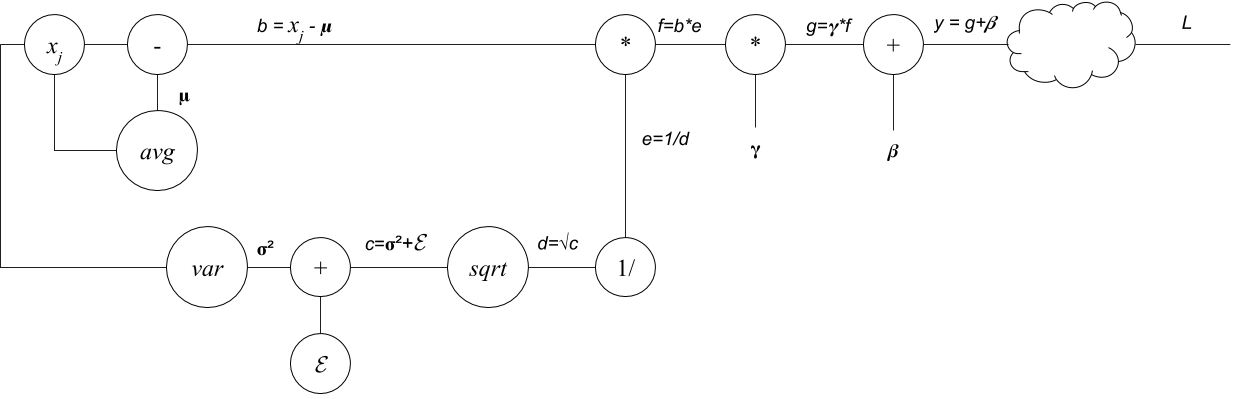Forward pass of the batch normalization.
Now lets start the backward propogation. We assume that we have recieved a \(N\times D\) matrix \(\frac{\partial L}{\partial y}\) from upstream. So lets calculate
\[\frac{\partial L}{\partial \beta}, \text{This will be a } D \text{ dimensional vector.} \nonumber\\ \frac{\partial L}{\partial g}, \text{This will be a } N \times D \text{ matrix.} \nonumber\]
and
\[\begin{align}\label{eqn:dg} \frac{\partial L}{\partial g} &= \frac{\partial L}{\partial y}\frac{\partial y}{\partial g} \nonumber \\ &= \frac{\partial L}{\partial y}\frac{\partial (g + \beta) }{\partial g} \nonumber \\ &= \frac{\partial L}{\partial y}, \text{This will be a } N \times D \text{ matrix.} \end{align}\]Sliding backward
and
\[\begin{align}\label{eqn:df} \frac{\partial L}{\partial f} &= \frac{\partial L}{\partial g}\frac{\partial g}{\partial f} \nonumber \\ &= \frac{\partial L}{\partial g}\frac{\partial (\gamma f)}{\partial f} \nonumber \\ &= \frac{\partial L}{\partial g}\gamma , \text{This will be a } N \times D \text{ matrix.} \end{align}\]Variance Stream
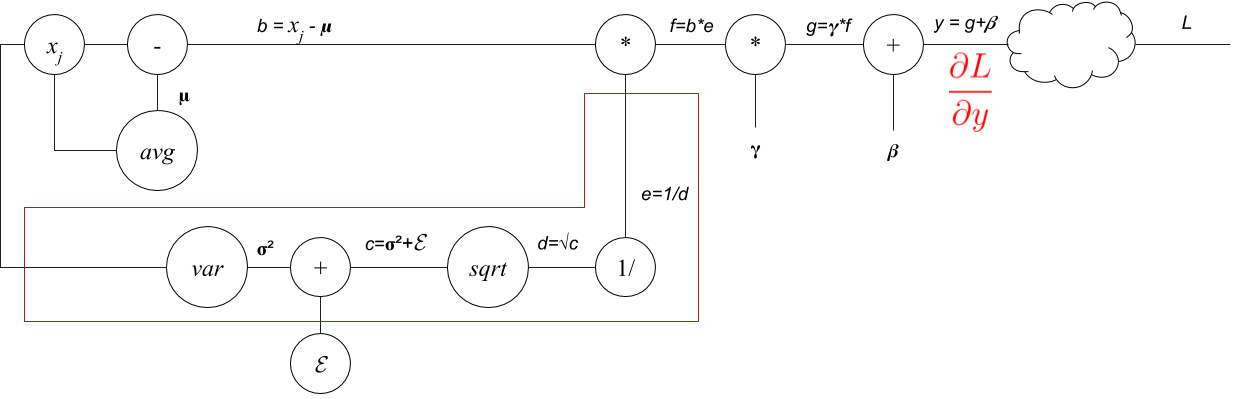
As we slide backward the stream gets broken into two. So lets first follow the variance stream back to its origin.
\[\begin{align} \frac{\partial L}{\partial e} &= \frac{\partial L}{\partial f}\frac{\partial f}{\partial e} \nonumber \\ &=\frac{\partial L}{\partial y}\gamma\frac{\partial (be)}{\partial e} \nonumber \\ &=\sum^{axis=0}\left(\frac{\partial L}{\partial y}\gamma b\right) , \text{This will be a } D \text{ dimensional vector.} \end{align}\] \[\begin{align} \frac{\partial L}{\partial d} &= \frac{\partial L}{\partial e} \frac{\partial e}{\partial d} \nonumber \\ &=\sum^{axis=0}\left(\frac{\partial L}{\partial y}\gamma b\right) \frac{\partial (\frac{1}{d})}{\partial d} \nonumber \\ &=-\sum^{axis=0}\left(\frac{\partial L}{\partial y}\gamma b\right) \frac{1}{d^{2}} , \text{This will be a } D \text{ dimensional vector.} \end{align}\] \[\begin{align} \frac{\partial L}{\partial c} &= \frac{\partial L}{\partial d}\frac{\partial d}{\partial c} \nonumber \\ & = -\sum^{axis=0}\left(\frac{\partial L}{\partial y}\gamma b\right) \frac{1}{d^{2}}\frac{\partial \sqrt{c}}{\partial c} \nonumber \\ & = -\sum^{axis=0}\left(\frac{\partial L}{\partial y}\gamma b\right) \frac{1}{d^{2}}\frac{1}{2}\frac{1}{\sqrt{c}} , \text{This will be a } D \text{ dimensional vector.} \end{align}\] \[\begin{align} \frac{\partial L}{\partial \sigma^2} &= \frac{\partial L}{\partial c}\frac{\partial c}{\partial \sigma^2} \nonumber \\ & = -\sum^{axis=0}\left(\frac{\partial L}{\partial y}\gamma b\right) \frac{1}{d^{2}}\frac{1}{2}\frac{1}{\sqrt{c}} \frac{\partial (\sigma^2 + \epsilon)}{\partial \sigma^2} \nonumber \\ & = -\sum^{axis=0}\left(\frac{\partial L}{\partial y}\gamma b\right) \frac{1}{d^{2}}\frac{1}{2}\frac{1}{\sqrt{c}}, \text{This will be a } D \text{ dimensional vector.} \end{align}\] \[\begin{align} \frac{\partial L}{\partial x} &= \frac{\partial L}{\partial \sigma^2}\frac{\partial \sigma^2}{\partial x}, \text{This will be a } N \times D \text{ matrix.} \end{align}\]This needs to be solved in an element-wise fashion. Lets focus on $x_{0,0}$ to get a sense of the what the result looks like.
\[\begin{align} \frac{\partial L}{\partial x_{0,0}} = \frac{\partial L}{\partial \sigma^2}\frac{\partial \sigma^2}{\partial x_{0,0}} \\ \end{align}\]Note that \(\frac{\partial L}{\partial \sigma^2}\) and \(\frac{\partial \sigma_0^2}{\partial x_{0,0}}\) are $D$ dimensional vectors.
\[\begin{align} \frac{\partial \sigma^2}{\partial x_{0,0}} = \begin{pmatrix} \frac{\partial \sigma_0^2}{\partial x_{0,0}} & \frac{\partial \sigma_1^2}{\partial x_{0,0}} & \dots & \frac{\partial \sigma_{D-2}^2}{\partial x_{0,0}} & \frac{\partial \sigma_{D-1}^2}{\partial x_{0,0}} \end{pmatrix} \end{align}\]Similar to Eq. \ref{eqn:sigma}, we know that
\[\begin{align} \sigma_{k}^2 = \frac{1}{N}\sum_{i=0}^{N-1}(x_{i,k} - \mu_{k})^2 \end{align}\]Using the equation above,
\[\begin{align} \frac{\partial \sigma^2}{\partial x_{0,0}} = \begin{pmatrix} \frac{2}{N} (x_{0,0} - \mu_0) & 0 & \dots & 0 & 0 \end{pmatrix} \end{align}\]Therefore
\[\begin{align} \frac{\partial L}{\partial x_{0,0}} &= \frac{\partial L}{\partial \sigma^2} \frac{\partial \sigma^2}{\partial x_{0,0}} \nonumber \\ & = \left(\frac{\partial L}{\partial \sigma^2}\right)_{0} \frac{2}{N} (x_{0,0} - \mu_0) \end{align}\]Rewiriting in a more readable format
\[\begin{align} \frac{\partial L}{\partial x_{0,0}} & = \frac{2}{N} (x_{0,0} - \mu_0) \left(\frac{\partial L}{\partial \sigma^2}\right)_{0} \end{align}\]We can similarly show that
\[\begin{align}\label{eqn:grad_L_x} \frac{\partial L}{\partial x_{k,j}} & = \frac{2}{N} (x_{k,j} - \mu_j) \left(\frac{\partial L}{\partial \sigma^2}\right)_{j} \end{align}\]where \(k \in N-1\) and \(j \in D-1\). We can rewrite the equation above in matrix form
\[\begin{align} \frac{\partial L}{\partial x} & = \frac{2}{N} (x - \mu) \frac{\partial L}{\partial \sigma^2} \end{align}\]Taking the result for \(\frac{\partial L}{\partial \sigma^2}\) into account.
\[\begin{align} \frac{\partial L}{\partial x} & = \frac{2}{N} (x - \mu) \left(-\sum^{axis=0}\left(\frac{\partial L}{\partial y}\gamma b\right) \frac{1}{d^{2}}\frac{1}{2}\frac{1}{\sqrt{c}}\right) \nonumber \\ & = -\frac{2}{N} (x - \mu) \left(\sum^{axis=0}\left(\frac{\partial L}{\partial y}\gamma b\right) \frac{1}{d^{2}}\frac{1}{2}\frac{1}{\sqrt{c}}\right) \end{align}\]This is the derivative from just one stream, now we need to follow the other stream.
The Other Stream
This needs to be broken down into its elements
\[\begin{align} \frac{\partial b}{\partial \mu_0} &= \begin{pmatrix} \frac{\partial(x_{0,0} - \mu_0)}{\partial \mu_{0}} & \frac{\partial(x_{0,1} - \mu_1)}{\partial \mu_{0}} & \dots & \frac{\partial(x_{0,D-2} - \mu_{D-2})}{\partial \mu_{0}} & \frac{\partial(x_{0,D-1} - \mu_{D-1})}{\partial \mu_{0}} \\ \frac{\partial(x_{1,0} - \mu_0)}{\partial \mu_{0}} & \frac{\partial(x_{1,1} - \mu_1)}{\partial \mu_{0}} & \dots & \frac{\partial(x_{1,D-2} - \mu_{D-2})}{\partial \mu_{0}} & \frac{\partial(x_{1,D-1} - \mu_{D-1})}{\partial \mu_{0}} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ \frac{\partial(x_{N-1,0} - \mu_0)}{\partial \mu_{0}} & \frac{\partial(x_{N-1,1} - \mu_1)}{\partial \mu_{0}} & \dots & \frac{\partial(x_{N-1,D-2} - \mu_{D-2})}{\partial \mu_{0}} & \frac{\partial(x_{N-1,D-1} - \mu_{D-1})}{\partial \mu_{0}} \end{pmatrix} \nonumber \\ &=\begin{pmatrix} -1 & 0 & \dots & 0 & 0 \\ -1 & 0 & \dots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ -1 & 0 & \dots & 0 & 0 \\ \end{pmatrix} \end{align}\]Note that even though \(\mu_0\) is dependent on \(x_{j,0}\) (where \(j \in D-1\)) we don’t need to take that into account here as it will come into play in the other stream backprop calculated in the next section.
\[\begin{align} \frac{\partial b}{\partial \mu_0} &= -\sum_{i=0}^{N-1}\left(\frac{\partial L}{\partial b}\right)_{i,0} \end{align}\]and
\[\begin{align}\label{eq:grad_L_mu} \frac{\partial L}{\partial \mu} &=-\sum^{axis=0}\left(\frac{\partial L}{\partial y}\gamma e\right) \end{align}\] \[\begin{align} \frac{\partial L}{\partial x} &= \frac{\partial L}{\partial \mu}\frac{\partial \mu}{\partial x}, \text{This will be a } N \times D \text{ matrix.} \end{align}\]This also need to be solved in an element wise fashion
\[\begin{align} \frac{\partial \mu}{\partial x_{0,0}} &= \begin{pmatrix} \frac{\partial \mu_0}{\partial x_{0,0}} & \frac{\partial \mu_1}{\partial x_{0,0}} & \dots & \frac{\partial \mu_{D-2}}{\partial x_{0,0}} & \frac{\partial \mu_{D-1}}{\partial x_{0,0}} \end{pmatrix} \nonumber \\ &= \begin{pmatrix} 1/N & 0 & \dots & 0 & 0 \end{pmatrix} \end{align}\]Therefore
\[\begin{align} \frac{\partial L}{\partial x_{0,0}} &= \frac{1}{N}\left( \frac{\partial L}{\partial \mu} \right)_{0,0} \end{align}\]It can be similary shown that
\[\begin{align} \frac{\partial \mu}{\partial x_{k,0}} &= \begin{pmatrix} 1/N & 0 & \dots & 0 & 0 \end{pmatrix} \\ \frac{\partial \mu}{\partial x_{k,1}} &= \begin{pmatrix} 0 & 1/N & \dots & 0 & 0 \end{pmatrix} \\ \frac{\partial \mu}{\partial x_{k,D-2}} &= \begin{pmatrix} 0 & 0 & \dots & 1/N & 0 \end{pmatrix} \\ \frac{\partial \mu}{\partial x_{k,D-1}} &= \begin{pmatrix} 0 & 0 & \dots & 0 & 1/N \end{pmatrix} \end{align}\]Therefore
\[\begin{align} \frac{\partial L}{\partial x} &= \frac{1}{N}\left(\frac{\partial L}{\partial \mu}\right) \end{align}\]and using Eq. \ref{eq:grad_L_mu}
\[\begin{align}\label{eqn:grad_l_x_stream2} \frac{\partial L}{\partial x} &= -\frac{1}{N}\sum^{axis=0}\left(\frac{\partial L}{\partial y}\gamma e\right) \\ \end{align}\]The Last Stream
This also needs to be looked at in an element wise fashion
\[\begin{align} \frac{\partial b}{\partial x_{0,0}} &= \begin{pmatrix} \frac{\partial(x_{0,0} - \mu_0)}{\partial x_{0,0}} & \frac{\partial(x_{0,1} - \mu_1)}{\partial x_{0,0}} & \dots & \frac{\partial(x_{0,D-2} - \mu_{D-2})}{\partial x_{0,0}} & \frac{\partial(x_{0,D-1} - \mu_{D-1})}{\partial x_{0,0}} \\ \frac{\partial(x_{1,0} - \mu_0)}{\partial x_{0,0}} & \frac{\partial(x_{1,1} - \mu_1)}{\partial x_{0,0}} & \dots & \frac{\partial(x_{1,D-2} - \mu_{D-2})}{\partial x_{0,0}} & \frac{\partial(x_{1,D-1} - \mu_{D-1})}{\partial \mu_{0}} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ \frac{\partial(x_{N-1,0} - \mu_0)}{\partial x_{0,0}} & \frac{\partial(x_{N-1,1} - \mu_1)}{\partial x_{0,0}} & \dots & \frac{\partial(x_{N-1,D-2} - \mu_{D-2})}{\partial x_{0,0}} & \frac{\partial(x_{N-1,D-1} - \mu_{D-1})}{\partial x_{0,0}} \end{pmatrix} \nonumber \\ &=\begin{pmatrix} 1 & 0 & \dots & 0 & 0 \\ 0 & 0 & \dots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \dots & 0 & 0 \\ \end{pmatrix} \end{align}\]Note that even though \(x_{0,0}\) is used to calculate \(\mu_0\) we don’t need to worry about that here as we already took that into account when deriving Eq. \ref{eqn:grad_l_x_stream2}. Using the equation above we can see that
\[\begin{align} \frac{\partial L}{\partial x_{0,0}} &= \left(\frac{\partial L}{\partial b}\right)_{0,0} \\ \end{align}\]Using Eq. \ref{eqn:grad_L_b} the matrix form emerges clearly
\[\begin{align} \frac{\partial L}{\partial x} &= \frac{\partial L}{\partial b} \nonumber \\ &= \frac{\partial L}{\partial y}\gamma e \end{align}\]Sum all the Streams
Now we can sum all the streams and obtain the following result without any simplification
\[\begin{align} \frac{\partial L}{\partial x} &= -\frac{2}{N} (x - \mu) \left(\sum^{axis=0}\left(\frac{\partial L}{\partial y}\gamma b\right) \frac{1}{d^{2}}\frac{1}{2}\frac{1}{\sqrt{c}}\right) -\frac{1}{N}\sum^{axis=0}\left(\frac{\partial L}{\partial y}\gamma e\right) +\frac{\partial L}{\partial y}\gamma e \end{align}\]Implementing these results in python:
def batchnorm_backward(dout, cache):
dgamma = np.sum(dout*cache['x_norm'], axis = 0)
dbeta = np.sum(dout, axis = 0)
# Using the cache from forward
x = cache['x']
mu = cache['sample_mean']
sigma = cache['sample_var']
eps = cache['eps']
gamma = cache['gamma']
beta = cache['beta']
N = cache['N']
b = x - mu
c = sigma + eps
d = np.sqrt(c)
e = 1/d
f = b*e
g = gamma*f
y = g + beta
dx = -(2/N)*(x-mu)*np.sum( dout*gamma*b*(1/d**2)*(1/2)*(1/np.sqrt(c)) , axis = 0) - (1/N)*np.sum( dout*gamma*e , axis = 0) + dout*gamma*e
return dx, dgamma, dbeta
Alternative Derivation of Batch Normalization Backward Propogation
A simpler way of calculating the backprop derivative for batch normalization is to take the derivative of Eq. \ref{eqn:bn}.
\[\begin{align} \frac{\partial L}{\partial x} &= \frac{\partial L}{\partial y}\frac{\partial y}{\partial x} \nonumber \\ &= \frac{\partial L}{\partial y}\frac{\partial(\gamma \hat{x} + \beta)}{\partial x} \nonumber \\ &=\frac{\partial L}{\partial y}\frac{\partial(\gamma \hat{x})}{\partial x} \nonumber \\ &=\left(\frac{\partial L}{\partial y}\gamma\right)\frac{\partial\hat{x}}{\partial x} \end{align}\]For simplicity, I will use the matrix given in Eq. \ref{eqn:xhat} for this derivation. Lets look at \(\frac{\partial \hat{x}}{\partial x_{0,0}}\) first to get a sense what the solution would look like:
\[\begin{align} \frac{\partial \hat{x}}{\partial x_{0,0}} &= \begin{pmatrix} \frac{\partial\left( \frac{x_{0,0} - \mu_{0}}{\sqrt{\sigma_{0}^2 + \epsilon}} \right) }{\partial x_{0,0}} & \frac{\partial\left( \frac{x_{0,1} - \mu_{1}}{\sqrt{\sigma_{1}^2 + \epsilon}} \right) }{\partial x_{0,0}} & \frac{\partial\left( \frac{x_{0,2} - \mu_{2}}{\sqrt{\sigma_{2}^2 + \epsilon}} \right) }{\partial x_{0,0}} & \frac{\partial\left( \frac{x_{0,3} - \mu_{3}}{\sqrt{\sigma_{3}^2 + \epsilon}} \right) }{\partial x_{0,0}} & \frac{\partial\left( \frac{x_{0,4} - \mu_{4}}{\sqrt{\sigma_{4}^2 + \epsilon}} \right) }{\partial x_{0,0}} \\ \frac{\partial\left( \frac{x_{1,0} - \mu_{0}}{\sqrt{\sigma_{0}^2 + \epsilon}} \right) }{\partial x_{0,0}} & \frac{\partial\left( \frac{x_{1,1} - \mu_{1}}{\sqrt{\sigma_{1}^2 + \epsilon}} \right) }{\partial x_{0,0}} & \frac{\partial\left( \frac{x_{1,2} - \mu_{2}}{\sqrt{\sigma_{2}^2 + \epsilon}} \right) }{\partial x_{0,0}} & \frac{\partial\left( \frac{x_{1,3} - \mu_{3}}{\sqrt{\sigma_{3}^2 + \epsilon}} \right) }{\partial x_{0,0}} & \frac{\partial\left( \frac{x_{1,4} - \mu_{4}}{\sqrt{\sigma_{4}^2 + \epsilon}} \right) }{\partial x_{0,0}} \\ \frac{\partial\left( \frac{x_{2,0} - \mu_{0}}{\sqrt{\sigma_{0}^2 + \epsilon}} \right) }{\partial x_{0,0}} & \frac{\partial\left( \frac{x_{2,1} - \mu_{1}}{\sqrt{\sigma_{1}^2 + \epsilon}} \right) }{\partial x_{0,0}} & \frac{\partial\left( \frac{x_{2,2} - \mu_{2}}{\sqrt{\sigma_{2}^2 + \epsilon}} \right) }{\partial x_{0,0}} & \frac{\partial\left( \frac{x_{2,3} - \mu_{3}}{\sqrt{\sigma_{3}^2 + \epsilon}} \right) }{\partial x_{0,0}} & \frac{\partial\left( \frac{x_{2,4} - \mu_{4}}{\sqrt{\sigma_{4}^2 + \epsilon}} \right) }{\partial x_{0,0}} \end{pmatrix} \nonumber\\ &= \begin{pmatrix} \frac{\partial\left( \frac{x_{0,0} - \mu_{0}}{\sqrt{\sigma_{0}^2 + \epsilon}} \right) }{\partial x_{0,0}} & 0 & 0 & 0 & 0 \\ \frac{\partial\left( \frac{x_{1,0} - \mu_{0}}{\sqrt{\sigma_{0}^2 + \epsilon}} \right) }{\partial x_{0,0}} & 0 & 0 & 0 & 0 \\ \frac{\partial\left( \frac{x_{2,0} - \mu_{0}}{\sqrt{\sigma_{0}^2 + \epsilon}} \right) }{\partial x_{0,0}} & 0 & 0 & 0 & 0 \end{pmatrix} \\ \end{align}\]Solving the first element of the matrix above using the quotient rule
\[\begin{align} \frac{\partial\left( \frac{x_{0,0} - \mu_{0}}{\sqrt{\sigma_{0}^2 + \epsilon}} \right) }{\partial x_{0,0}} = &=\frac{ \sqrt{ \sigma_{0}^{2} + \epsilon } \frac{\partial \left(x_{0,0} - \mu_0 \right)}{\partial x_{0,0}} - \left(x_{0,0} - \mu_0 \right) \frac{\partial \sqrt{ \sigma_{0}^{2} + \epsilon }}{\partial x_{0,0}} } {\left(\sqrt{\sigma_{0}^2 + \epsilon}\right)^2} \nonumber \\ &=\frac{ \sqrt{ \sigma_{0}^{2} + \epsilon } \left(1 - \frac{1}{N}\right) - \left(x_{0,0} - \mu_0 \right)\frac{1}{2}\frac{1}{\sqrt{\sigma_{0}^{2} + \epsilon}} \frac{2}{N}( x_{0,0} - \mu_0 ) }{\sigma_{0}^2 + \epsilon} \nonumber \\ &=\frac{ \sqrt{ \sigma_{0}^{2} + \epsilon } \left(1 - \frac{1}{N}\right) - \frac{1}{N}\frac{1}{\sqrt{\sigma_{0}^{2} + \epsilon}}\left(x_{0,0} - \mu_0 \right)( x_{0,0} - \mu_0 ) }{\sigma_{0}^2 + \epsilon} \end{align}\]We can simlary show that
\[\begin{align} \frac{\partial\left( \frac{x_{1,0} - \mu_{0}}{\sqrt{\sigma_{0}^2 + \epsilon}} \right) }{\partial x_{0,0}} =\frac{ \sqrt{ \sigma_{0}^{2} + \epsilon } \left(- \frac{1}{N}\right) - \frac{1}{N}\frac{1}{\sqrt{\sigma_{0}^{2} + \epsilon}}\left(x_{1,0} - \mu_0 \right)( x_{0,0} - \mu_0 ) }{\sigma_{0}^2 + \epsilon} \\ \frac{\partial\left( \frac{x_{2,0} - \mu_{0}}{\sqrt{\sigma_{0}^2 + \epsilon}} \right) }{\partial x_{0,0}} =\frac{ \sqrt{ \sigma_{0}^{2} + \epsilon } \left( - \frac{1}{N}\right) - \frac{1}{N}\frac{1}{\sqrt{\sigma_{0}^{2} + \epsilon}}\left(x_{2,0} - \mu_0 \right)( x_{0,0} - \mu_0 ) }{\sigma_{0}^2 + \epsilon} \end{align}\]For simplicity let
\[\begin{align} v_0 = \sigma_0^2 + \epsilon \end{align}\]The derivative \(\frac{\partial L}{\partial x_{0,0}}\) can now be given as
\[\begin{align} \frac{\partial L}{\partial x_{0,0}} =& \sum_{i=0}^{2}\left(\frac{\partial L}{\partial y}\gamma\right)_{i,0} \left(\frac{\partial \hat{x}}{\partial x_{0,0}}\right)_{i,0} \nonumber \\ =&\left(\frac{\partial L}{\partial y}\gamma\right)_{0,0} \frac{ \sqrt{ v_0 } \left(1 - \frac{1}{N}\right) - \frac{1}{N}\frac{1}{\sqrt{v_0}}\left(x_{0,0} - \mu_0 \right)( x_{0,0} - \mu_0 ) }{v} \nonumber \\ &+\left(\frac{\partial L}{\partial y}\gamma\right)_{1,0} \frac{ \sqrt{ v_0 } \left(- \frac{1}{N}\right) - \frac{1}{N}\frac{1}{\sqrt{v_0}}\left(x_{1,0} - \mu_0 \right)( x_{0,0} - \mu_0 ) }{v} \nonumber \\ &+\left(\frac{\partial L}{\partial y}\gamma\right)_{2,0} \frac{ \sqrt{ v_0 } \left( - \frac{1}{N}\right) - \frac{1}{N}\frac{1}{\sqrt{v_0}}\left(x_{2,0} - \mu_0 \right)( x_{0,0} - \mu_0 ) }{v} \nonumber \\ =& \left(\frac{\partial L}{\partial y}\gamma\right)_{0,0}\frac{1}{\sqrt{v_0}} + \frac{-1}{N(\sqrt{v})}\sum_{i=0}^{2}\left(\frac{\partial L}{\partial y}\gamma\right)_{i,0} \nonumber \\ &+ \frac{-1}{N(v_0^{3/2})}( x_{0,0} - \mu_0 )\sum_{i=0}^{2}\left(\frac{\partial L}{\partial y}\gamma\right)_{i,0} ( x_{i,0} - \mu_0 ) \nonumber \\ =& \left(\frac{\partial L}{\partial y}\gamma\right)_{0,0}\frac{1}{\sqrt{v_0}} \nonumber \\ &+ \frac{1}{v_0^{3/2}} \left( \frac{-v_0}{N}\sum_{i=0}^{2}\left(\frac{\partial L}{\partial y}\gamma\right)_{i,0} + \frac{-1}{N}( x_{0,0} - \mu_0 )\sum_{i=0}^{2}\left(\frac{\partial L}{\partial y}\gamma\right)_{i,0} ( x_{i,0} - \mu_0 ) \right) \end{align}\]We can similarly show that,
\[\begin{align} \frac{\partial L}{\partial x_{k,j}} =& \left(\frac{\partial L}{\partial y}\gamma\right)_{k,j}\frac{1}{\sqrt{v_j}} \nonumber \\ &+ \frac{1}{Nv_j^{3/2}} \left( -v_j\sum_{j=0}^{N-1}\left(\frac{\partial L}{\partial y}\gamma\right)_{k,j} - ( x_{k,j} - \mu_0 )\sum_{j=0}^{N-1}\left(\frac{\partial L}{\partial y}\gamma\right)_{k,j} ( x_{k,j} - \mu_j ) \right) \end{align}\]where \(k \in N-1\) and \(j \in D-1\). We can write the result above in matrix form:
\[\begin{align} \frac{\partial L}{\partial x} =& \left(\frac{\partial L}{\partial y}\gamma\right)\frac{1}{\sqrt{v}} \nonumber \\ &+ \frac{1}{Nv^{3/2}} \left( -v\sum^{axis=0}\left(\frac{\partial L}{\partial y}\gamma\right) - ( x - \mu )\sum^{axis=0}\left(\frac{\partial L}{\partial y}\gamma\right) ( x - \mu ) \right) \end{align}\]This result can be implemented in python as follows:
def batchnorm_backward_alt(dout, cache):
dgamma = np.sum(dout * cache['x_norm'], axis=0)
dbeta = np.sum(dout, axis=0)
v = cache['sample_var'] + cache['eps']
dx = cache['gamma'] * (dout / v ** (1 / 2) - \
(1 / ((cache['N'] * v ** (3 / 2)))) * (np.sum(dout * v, axis=0) + (cache['x'] - cache['sample_mean'])
* np.sum(dout * (cache['x'] - cache['sample_mean']),axis=0) ) )
return dx, dgamma, dbeta
The alternative derivative calculation is ~1.2x faster than the derivative calculated using back propogation.
Layer Normalization
Layer normalization is similar to batch normalization except in layer normalization mean and variance is calculated over sample axis instead of feature axis. The forward pass and backward pass for layer normalization is calculated the same way as well.
Layernorm forward pass:
def layernorm_forward(x, gamma, beta, ln_param):
out, cache = None, None
eps = ln_param.get('eps', 1e-5)
sample_mean = x.mean(axis=1)
sample_var = x.var(axis=1)
x_norm = ((x.T - sample_mean) / np.sqrt(sample_var + eps)).T
out = gamma * x_norm + beta
cache = {}
cache['gamma'] = gamma
cache['beta'] = beta
cache['x_norm'] = x_norm
cache['x'] = x
cache['sample_mean'] = sample_mean
cache['sample_var'] = sample_var
cache['eps'] = eps
cache['N'], cache['D'] = x.shape
return out, cache
The backward pass formula will be
\[\begin{align} \frac{\partial L}{\partial x} =& \left(\frac{\partial L}{\partial y}\gamma\right)\frac{1}{\sqrt{v}} \nonumber \\ &+ \frac{1}{Nv^{3/2}} \left( -v\sum^{axis=1}\left(\frac{\partial L}{\partial y}\gamma\right) - ( x - \mu )\sum^{axis=1}\left(\frac{\partial L}{\partial y}\gamma\right) ( x - \mu ) \right) \end{align}\]and in Python
def layernorm_backward(dout, cache):
dx, dgamma, dbeta = None, None, None
for k, v in cache.items():
try:
print(k, v.shape)
print(v)
except:
pass
dgamma = np.sum(dout * cache['x_norm'], axis=0)
dbeta = np.sum(dout, axis=0)
v = cache['sample_var'] + cache['eps']
dx = ( (cache['gamma'] * dout).T / v ** (1 / 2) ) - ((1 / ((cache['D'] * v ** (3 / 2))))*(\
np.sum(dout * cache['gamma'], axis=1)*v + (cache['x'].T - cache['sample_mean'])* \
np.sum( (dout*cache['gamma']).T * (cache['x'].T - cache['sample_mean']), axis=0)) )
return dx.T, dgamma, dbeta
Check out the full assignment here
Comments