How to determine if the point is inside the rectangle?

While working on a problem recently I had to figure out how to find if a point is inside a non-axis aligned rectangle. After doing a bit of research online I found that there are a few ways of solving this problem. One very simple way to solve this problem is to split the rectangle into 4 triangles, this solution is described wonderfully here.

This solution still looks like a lot of work for a rather simple problem. After doing a bit of research I came across this answer on stackexchange. The answer looks really simple and elegant but the author doesn’t provide any explanation for the result. After a bit of thinking I have figured out why the solution that the author provided works.

Dot Product as Projection

Imagine you have 2 vectors $\vec{AB}$ and $\vec{AP}$. The scalar projection of the vector $\vec{AP}$ in the direction of vector $\vec{AB}$ is given by

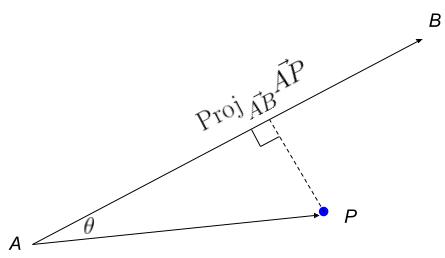Projection of point $P$ onto vector $\vec{AB}$.

$ \begin{align} \text{Proj}_{\vec{AB}}\vec{AP} = \lVert\vec{AP}\lVert \text{cos} \theta \end{align} $

where $\lVert\vec{AP}\lVert$ is the Euclidean length of the vector $\vec{AP}$ and $\theta$ is the angle between the vectors $\vec{AB}$ and $\vec{AP}$.

Dot product of the vector $\vec{AB}$ and $\vec{AP}$ is defined as

$ \begin{align} \vec{AB} \cdot \vec{AP} = \lVert\vec{AB}\lVert \lVert\vec{AP}\lVert \text{cos} \theta \end{align} $

we can use dot product definition to rewrite scalar projection of the vector $\vec{AP}$ in the direction of vector $\vec{AB}$ as

\[\begin{align} \text{Proj}_{\vec{AB}}\vec{AP} &= \lVert\vec{AP}\lVert \text{cos} \theta \\ &= \dfrac{\vec{AB} \cdot \vec{AP}}{\lVert\vec{AB}\lVert} \end{align}\]

Using Projection to Determine Point in a Rectangle

Now lets get back to the point in a rectangle problem. Lets start with a rectangle whose four coreners are given by $A$, $B$, $C$ and $D$. We will also have a point $P$. Lets also imagine a theoretical point that is on top on the point $B$.

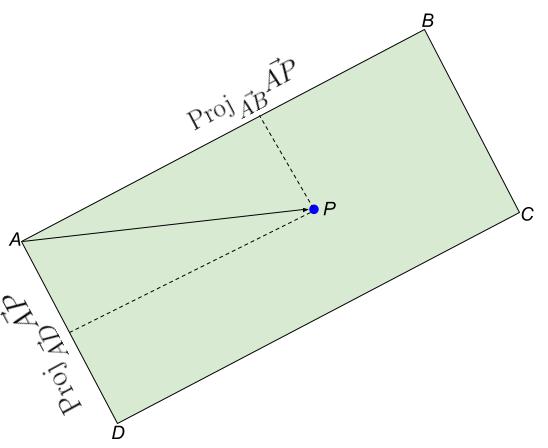Projection of point $P$ onto vectors $\vec{AB}$ and $\vec{AD}$.

The vector $\vec{AP}$ projects on to $\vec{AB}$ iff

$ \begin{align} 0 \leq \text{Proj}_{\vec{AB}}\vec{AP} \leq \text{Proj}_{\vec{AB}}\vec{AB} \end{align} $

Similarly the vector $\vec{AP}$ projects on to $\vec{AD}$ iff

$ \begin{align} 0 \leq \text{Proj}_{\vec{AB}}\vec{AP} \leq \text{Proj}_{\vec{AD}}\vec{AD} \end{align} $

So the point $P$ is inside the rectangle iff

$ \begin{align}\label{eq:in_rectangle} 0 \leq \text{Proj}_{\vec{AB}}\vec{AP} \leq \text{Proj}_{\vec{AB}}\vec{AB} \text{ and } 0 \leq \text{Proj}_{\vec{AD}}\vec{AP} \leq \text{Proj}_{\vec{AD}}\vec{AD} \end{align} $

Now that we have an understanding of how we can find if a point is inside a rectangle can be resolved using projections, lets rewrite Eq.~\ref{eq:in_rectangle} using dot product

$ \begin{align}\label{eq:in_rectangle_dot} 0 \leq \dfrac{\vec{AB} \cdot \vec{AP}}{\lVert\vec{AB}\lVert} \leq \dfrac{\vec{AB} \cdot \vec{AB}}{\lVert\vec{AB}\lVert} \text{ and } 0 \leq \dfrac{\vec{AD} \cdot \vec{AP}}{\lVert\vec{AD}\lVert} \leq \dfrac{\vec{AD} \cdot \vec{AD}}{\lVert\vec{AD}\lVert} \end{align} $

It is quite obvious that Eq.~\ref{eq:in_rectangle_dot} can be simplified further as

$ \begin{align} 0 \leq \vec{AB} \cdot \vec{AP} \leq \vec{AB} \cdot \vec{AB} \text{ and } 0 \leq \vec{AD} \cdot \vec{AP} \leq \vec{AD} \cdot \vec{AD} \end{align} $

References:

1. Raymond Manzoni (https://math.stackexchange.com/users/21783/raymond-manzoni), How to check if a point is inside a rectangle?, URL (version: 2012-09-03): https://math.stackexchange.com/q/190373
2. Nykamp DQ, “The formula for the dot product in terms of vector components.” From Math Insight. http://mathinsight.org/dot_product_formula_components