Dropout Regularization -- CS231n Exercise

I am currently working my way through the lectures for CS231n: Convolutional Neural Networks for Visual Recognition. I will post my solutions here.

Dropout is regularization technique where randomly selected output activations are set to zero during the forward pass. This prevents co-adaptations where features are only useful when present in the presence of other features.

Dropout – Forward

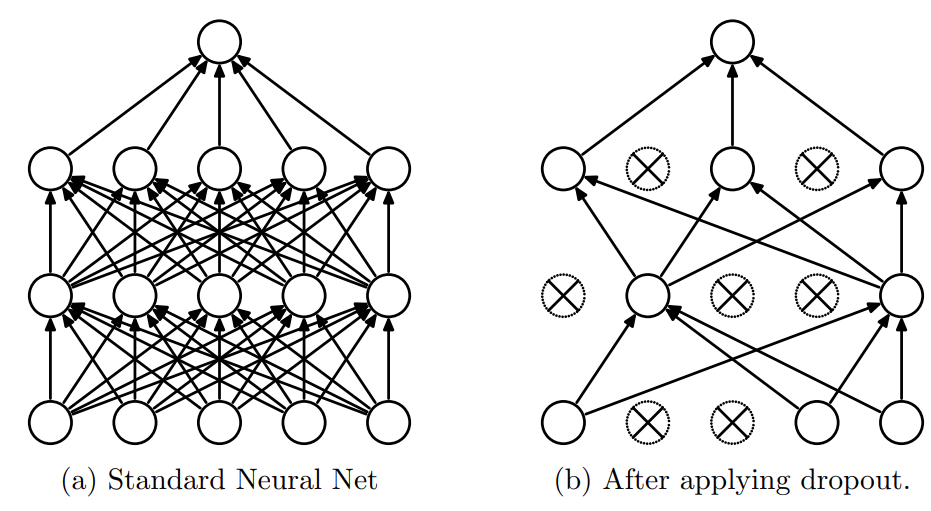From the dropout paper by Srivastava et. al. Dropout can be thought of as removing connections between layers.

In the figure above dropout is presented as dropping connections between layers. In matrix form, we can implement dropout by zeroing elements of the matrix in the layer.

For example if we have a layer \(h^{(t)}\) that we want to apply dropout to then we create a mask matrix with same dimensions as \(h^{(t)}\) with probability of any element of the mask being 0 is \(p\). The subsequent layer is caluclated thus

where \(\odot\) signifies element wise multiplication.

In python this can be implemented as

mask = (np.random.rand(*x.shape) < p) # dropout mask.
out = x * mask  # drop!

This procedure is what we follow at training time but when testing or actually using the neural network trained with dropout in production we need to take account of dropout in a different way. We want the expected value of the neuron during testing to reflect their expected value at training. At the training the expected value of any element of \(h^{(t)}_{i,j}\) will be \(p*h^{(t)}_{i,j}\) with dropout. We want to revert the values of neurons at testing to this expected value without applying dropout. We can do this by just muliplying all elements of \(h_{(t)}\) by \(p\) during testing.

out = x * p

In the assignment we are asked to implement dropout in a slightly different way, divide the output during training by \(p\) so that we don’t have to do the multiplication during testing. Here is how I implemented this:

def dropout_forward(x, dropout_param):
    p, mode = dropout_param['p'], dropout_param['mode']
    if 'seed' in dropout_param:
        np.random.seed(dropout_param['seed'])

    mask = None
    out = None

    if mode == 'train':
        mask = (np.random.rand(*x.shape) < p) / p # dropout mask.
        out = x * mask  # drop!
    elif mode == 'test':
        out = x
    cache = (dropout_param, mask)
    out = out.astype(x.dtype, copy=False)

    return out, cache

Dropout – Backward

Backward propogation over the dropout layer is rather simple to calculate because we are dealing with element-wise multiplication.

In Python this can be implemented as follows

def dropout_backward(dout, cache):
    dropout_param, mask = cache
    mode = dropout_param['mode']

    dx = None
    if mode == 'train':
        dx = dout * mask
    elif mode == 'test':
        dx = dout
    return dx

Check out the full assignment here