In this exercise we are asked to implement a vanilla implementation of Recurrent Neural Networks (RNN) for image captioning. We will be using the Microsoft COCO data set to try it our algorithm.
I am going to skip over the setup as it is clearly explained in the assignment notes and jump to the math that needs to be derived to implement the forward and backward pass of RNN.
RNN – Forward
The forward pass of the RNN is easy to implement. We need to apply the recurrent formula on the incoming state (\(h_{t-1}\)) to get the current state (\(h_t\)).
\[h_t = f_W (h_{t-1}, x_t)\]where \(f_W\) is some activation function with parameters \(W\) and \(x_t\) is the input vector at time step. Here is a pictorial representation of an RNN cell at sequence \(t\):
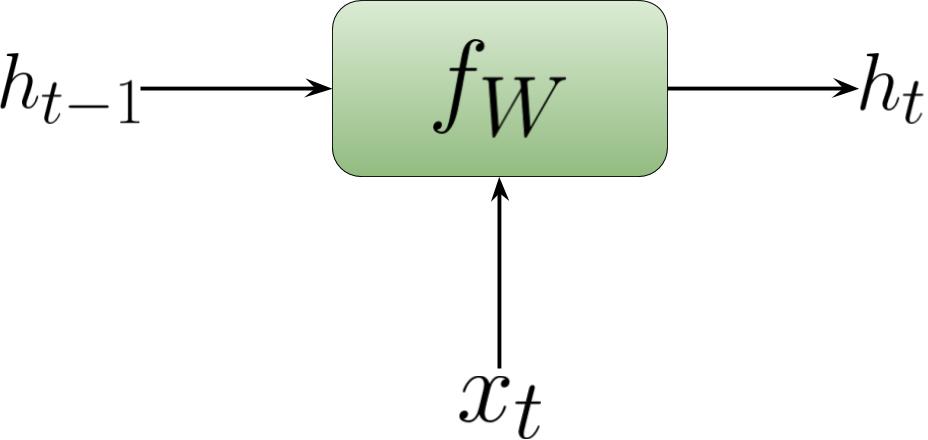A look at the forward operation of the RNN cell.
Here is a break down of what is actually happening inside the RNN cell.
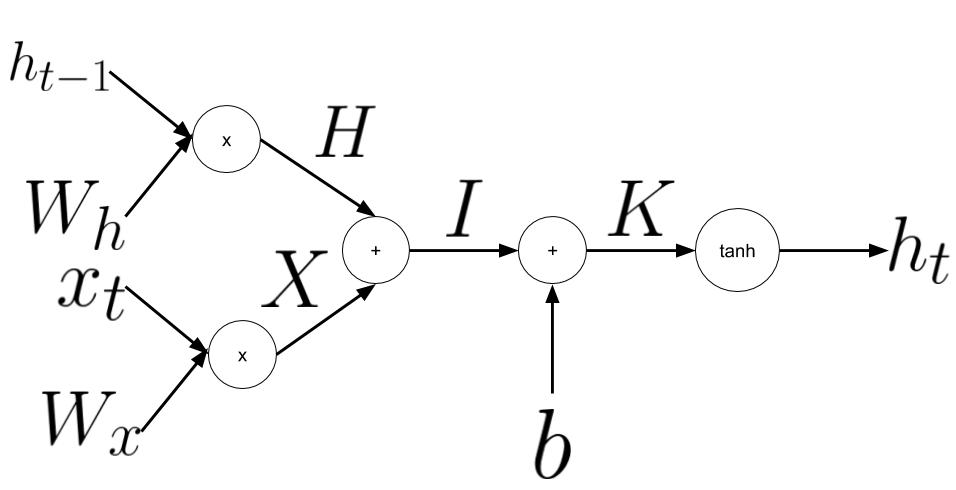A look at the operation performed inside the RNN cell the function \(f_W\).
In the vanilla implementation of the forward pass we will use tanh as the activation function, here is how I implemented this in python:
def rnn_step_forward(x, prev_h, Wx, Wh, b):
next_h = np.tanh(prev_h.dot(Wh) + x.dot(Wx) + b)
cache = (x, prev_h, Wx, Wh, b, next_h)
return next_h, cache
RNN – Backward
When performing the backward pass over the RNN, we start with the derivative coming in to the cell from upstream, step backward and take the derivative based the operation performed in the cell.
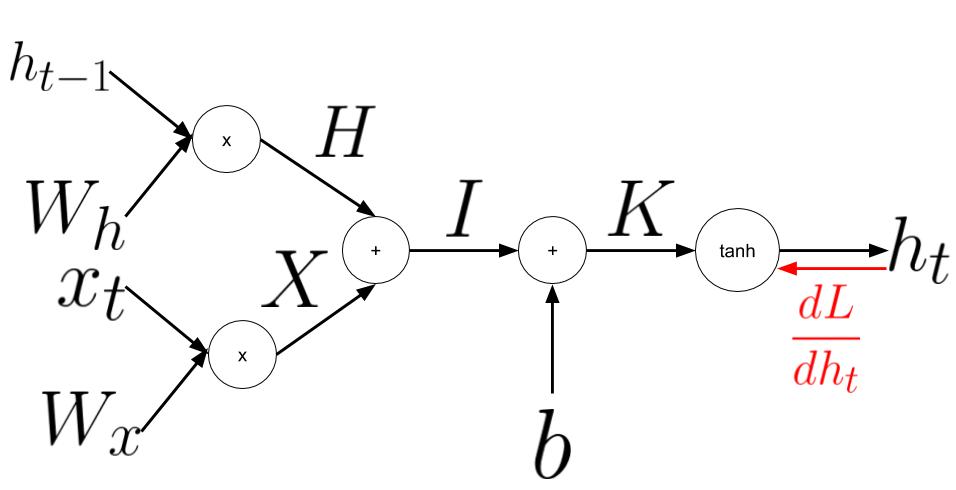We recieved a derivative from upstream \(\color{red} \frac{dL}{dh_t}\).
To preven clutter on the diagram I will write out the derivate of \(L\) with respect to each element shown in the diagram above down here:
\[\begin{align} \color{red}\frac{dL}{dK} &\color{red}= (1-h_t^2) \odot \frac{dL}{dh_t} \nonumber \\ \color{red}\frac{dL}{db} &\color{red}= \sum^{\text{axis=0}}\frac{dL}{dK} \nonumber \\ \color{red}\frac{dL}{dI} &\color{red}= \frac{dL}{dK} \nonumber \\ \end{align}\]where \(\odot\) denotes element-wise multiplication. Now lets first follow the derivative towards \(h_{t-1}\) and \(W_h\)
\[\begin{align} \color{red}\frac{dL}{dH} &\color{red}= \frac{dL}{dK} \nonumber \\ \color{red}\frac{dL}{dh_{t-1}} &\color{red}= \frac{dL}{dK}W_h^T \nonumber \\ \color{red}\frac{dL}{dW_h} &\color{red}= h_{t-1}^T\frac{dL}{dK} \nonumber \\ \end{align}\]Now lets go back to where we split and follow the backward stream to \(x_t\) and \(W_x\)
\[\begin{align} \color{red}\frac{dL}{dX} &\color{red}= \frac{dL}{dK} \nonumber \\ \color{red}\frac{dL}{dx_t} &\color{red}= \frac{dL}{dK}W_x^T \nonumber \\ \color{red}\frac{dL}{dW_x} &\color{red}= x_t^T\frac{dL}{dK} \nonumber \\ \end{align}\]Note that the subscript \(T\) denotes transpose.
In python we can implement this as follows:
def rnn_step_backward(dnext_h, cache):
(x, prev_h, Wx, Wh, b, next_h) = cache
dK = (1 - next_h**2)*dnext_h
dx = dK.dot(Wx.T)
dprev_h = dK.dot(Wh.T)
dWx = x.T.dot(dK)
dWh = prev_h.T.dot(dK)
db = np.sum(dK, axis=0)
return dx, dprev_h, dWx, dWh, db
The rest of the assignment is about implementing the RNN functions we have derived to image captioning. Check out the full assignment here
Comments