Training a Machine Learning Algorithm to Predict Stock Price Movement

01 Oct 2020 • Stocks

_config.yml Photo by Kevin Ku on Unsplash

It goes without saying that having a crystal ball that tells you whether the price of a stock is going to be higher or lower in the future will make you rich. A crystal ball is a pipe dream but it is possible to train a machine learning (ML) algorithm that can predict the stock price movement with reasonable accuracy. I have been looking for ML algorithms or technical indicators that will tell me good entry and exit points for a stock. For example, here is the Intel stock price chart for the period of 2016-02-23 to 2020-09-28.

Visually inspecting, I can see a couple of the points in time where I would have liked to have bought and sold Intel stocks.

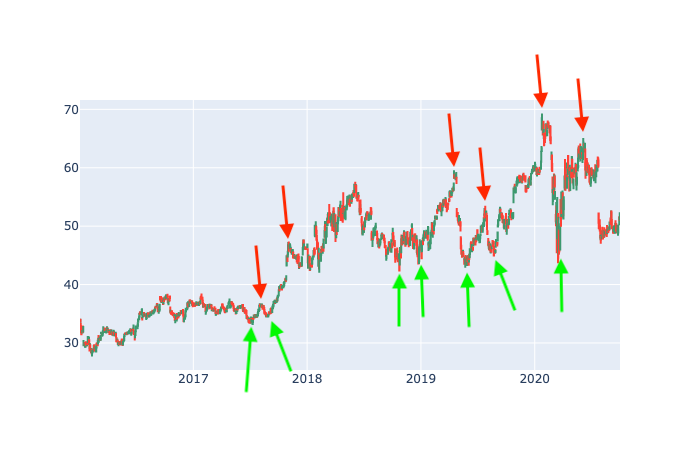
_config.yml

I would like to train an algorithm on these entry and exit points so that I can use it to identify these points in the future. Looking closely over the whole stock chart and exhaustively marking good entry and exit points is not feasible. It would be great to have a metric that is representative of the future action of a stock price.

After a bit of research, I came across a very interesting paper (see here) that details a method to generate a continuous metric for a stock chart. The metric is based on the future movement of the stock price, its range is between 0 and 1; where 0 is a strong sell signal while 1 is a strong buy signal.

Evaluating the Trading Signal Metric

The method to evaluate the trading signal is rather straight forward.

  • Calculate the 15-day moving average (MA) of the stock price.
  • If the current price is above 15-day MA and the price has been increasing consistently for the last 5-days then signal trend is UP.

  • If the current price is below 15-day MA and the price has been decreasing consistently for the last 5-days then signal trend is DOWN.

  • For UP trend, the trend signal is given by:
\[Tr_{i} = \frac{cp_i - \text{min } cp}{\text{max } cp - \text{min } cp} * 0.5 + 0.5\]

where

\[\text{min } cp = \text{min } (cp_i, cp_{i+1}, cp_{i+2}) \\ \text{max } cp = \text{max } (cp_i, cp_{i+1}, cp_{i+2})\]

For DOWN trend, the trend signal is given by:

\[Tr_{i} = \frac{cp_i - \text{min } cp}{\text{max } cp - \text{min } cp} * 0.5\]

Here is the Python code to generate the trading signal using this method. I am going to be using ta-lib, an incredibly fast wrapper for Python that includes 150+ technical indicators, to calculate the technical indicators needed to evaluate the metric.

import pandas as pd
import talib

df = pd.read_csv('INTC.csv')

df.Date = pd.to_datetime(df.Date)

df.sort_values(by='Date', inplace=True)

df['sma_15'] = talib.SMA(df['Adj Close'], timeperiod=15)

df['sma_15_diff'] = df['sma_15'].diff()

df['Trend'] = 'no'

start_ = min(df.index) + 20

for d, row in df[df.index > start_].iterrows():
    if sum(df[(df.index <= d) & (df.index > d - 5)].sma_15_diff < 0) == 5 and row['sma_15'] > row['Adj Close']:
        df.loc[d, 'Trend'] = 'down'
    elif sum(df[(df.index <= d) & (df.index > d - 5)].sma_15_diff > 0) == 5 and row['sma_15'] < row['Adj Close']:
        df.loc[d, 'Trend'] = 'up'
        
df['Trading Signal'] = 0

hold = 0

for d, row in df[df.index > start_].iterrows():
    try:
        min_ = min(df[(df.index >= d) & (df.index < d + 3)]['Adj Close'])
        max_ = max(df[(df.index >= d) & (df.index < d + 3)]['Adj Close'])
    except:
        print("Can't look ahead")
        break
    if max_ != min_:
        if row['Trend'] == 'up':
            hold = 0.5
            df.loc[d, 'Trading Signal'] = (row['Adj Close'] - min_)*0.5/(max_ - min_) + hold

        elif row['Trend'] == 'down':
            hold = 0
            df.loc[d, 'Trading Signal'] = (row['Adj Close'] - min_)*0.5/(max_ - min_) + hold
        else:
            df.loc[d, 'Trading Signal'] = (row['Adj Close'] - min_)*0.5/(max_ - min_) + hold

Lets see how good the metric performs on the Intel stock price chart:

As you can see, the metric captures entry and exit points really well.

Lets do Machine Learning

Now that we have a good metric that is predictive of the future movement of the stock price, we can fit a regression algorithm to predict this metric.

Identifying Features

Before fitting an ML algorithm we need to identify features that we think will be good at predicting a stock price movement. Constructing features to predict stock price movement is a very rich field, market watchers have constructed hundred of indicators that they swear by. Instead of spending months constructing features, we can just look up stock indicators that traders like and use them in our algorithm. Based on my research, I have decided to use the following stock indicators:

  1. Relative Change – Price
  2. Relative Change – Volume
  3. Relative Strength Index – Price
  4. Relative Strength Index – Volume
  5. Williams %R – Price
  6. Average Directional Movement Index – Price
  7. Chaikin Money Flow – Volume
  8. How much 14-Day Standard Deviation is the current closing price off by?
  9. How much 14-Day Standard Deviation is the current volume off by?

It is easy to calculate these indicators using the ta-lib wrapper:

def assignFactor(df):
                
    df['priceROC'] = (df['Adj Close'] - df['Adj Close'].shift(1))/df['Adj Close'].shift(1)
    df['volumeROC'] = (df['Volume'] - df['Volume'].shift(1))/df['Volume'].shift(1)

    
    df['RSIClose'] = talib.RSI(df['Adj Close'])
    df['RSIVolume'] = talib.RSI(df['Volume'])
    
    df['WILLR'] = talib.WILLR(df.High.values, df.Low.values, df.Close.values)
    
    df['ADX'] = talib.ADX(df['High'], df['Low'], df['Close'], timeperiod=14)
    
    # Volume indicator
    # CMF = n-day Sum of [(((C - L) - (H - C)) / (H - L)) x Vol] / n-day Sum of Vol
    cmf_hold = ( ( df['Close'] - df['Low'] ) - ( df['High'] - df['Close'] ) ) / ( df['High'] - df['Low'] ) * df['Volume']
    df['CMF'] = cmf_hold.rolling(14).sum()/df['Volume'].rolling(14).sum()
    del cmf_hold
        
    df['14DayStDevPrice'] = talib.STDDEV(df['Adj Close'], timeperiod=14, nbdev=1)

    df['upperbandPrice'], df['middlebandPrice'], df['lowerbandPrice'] = talib.BBANDS(df['Adj Close'], 
                                                            timeperiod=14, nbdevup=1, nbdevdn=1, matype=0)
    
    # How many standard deviations is the current price from 80-day moving average
    df['offBy14DayStDevPrice'] = ( df['Adj Close'] - df['middlebandPrice'] ) / df['14DayStDevPrice']
    
    df['14DayStDevVolume'] = talib.STDDEV(df['Volume'], timeperiod=14, nbdev=1)

    df['upperbandVolume'], df['middlebandVolume'], df['lowerbandVolume'] = talib.BBANDS(df['Volume'], 
                                                            timeperiod=14, nbdevup=1, nbdevdn=1, matype=0)
    
    # How many standard deviations is the current Volume from 80-day moving average
    df['offBy14DayStDevVolume'] = ( df['Volume'] - df['middlebandVolume'] ) / df['14DayStDevVolume']
    
    df.dropna(inplace=True)
    
    return df

Now lets split the data set into training, validation and testing set:

features = ['RSIClose', 'RSIVolume', 'WILLR', 'CMF', 'priceROC', 'volumeROC', 'ADX', 
            'offBy14DayStDevPrice', 'offBy14DayStDevVolume']

df_train = df[(df.Date >= '2016-01-01') & (df.Date < '2020-01-01') ]
y_train = df_train['Trading Signal'].values
df_train = df_train[features]
X_train = scaler.transform(df_train)

df_valid = df[(df.Date >= '2020-01-01') & (df.Date < '2020-04-01') ]
y_valid = df_valid['Trading Signal'].values
df_valid = df_valid[features]
X_valid = scaler.transform(df_valid)

df_test = df[(df.Date >= '2020-04-01') ]
y_test = df_test['Trading Signal'].values
df_test = df_test[features]
X_test = scaler.transform(df_test)

We have 9 features for training and the training set has 979 data points, the validation set has 83 data point and the test set has 106 data points.

Gradient Boosted Regression

After trying a couple of different algorithms, I found that the gradient boosted regression (gbr) performs the best. In this section I will cover how to optimized the gbr algorithm. Firstly, use random search to narrow down the range of combinations of gbr parameters that need to be optimize.

import numpy as np
import random
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_squared_error

best_mse = 1e99

for i in range(500):
    loss = random.choice(['ls', 'lad', 'huber', 'quantile'])
    learning_rate = np.random.random(1)[0]
    n_estimators = np.random.randint(2, 50)
    criterion = random.choice(['friedman_mse', 'mse', 'mae'])
    min_samples_split = np.random.randint(2, 50)
    min_samples_leaf = np.random.randint(2, 50)
    max_depth = np.random.randint(2, 50)
        
    gbr = GradientBoostingRegressor(loss=loss, learning_rate=learning_rate, n_estimators=n_estimators, 
                         criterion=criterion, min_samples_split=min_samples_split, min_samples_leaf=min_samples_leaf, 
                                        max_depth=max_depth)
    
    gbr.fit(X_train, y_train)
    
    print('Done iteration: ', i)
    
    y_pred = gbr.predict(X_test)
    mse = mean_squared_error(y_test, y_pred)
    
    print('mse: ', mse)
    
    if mse < best_mse:
        best_mse = mse
        best_loss= loss
        best_learning_rate = learning_rate
        best_n_estimators = n_estimators
        best_criterion = criterion
        best_min_samples_split = min_samples_split
        best_min_samples_leaf = min_samples_leaf
        best_max_depth = max_depth
        best_gbr = gbr

We get a mean squared error of 0.06734 on the validation set following random search. Lets see if this error can be reduced further by performing grid search around the best parameters found using random search.

params = ['max_depth', 'min_samples_leaf', 'min_samples_split', 
         'n_estimators']

param_grid = {}

for p in params:
    val = eval(f'best_{p}')
    if val > 5:
        param_grid[p] = np.arange(val - 4, val + 6, 2)
    else:
        param_grid[p] = np.arange(2, 6)

print(param_grid)
        
# Use gridsearch to find the best parameters
i=1
# for criterion in param_grid['criterion']:
# for max_features in param_grid['max_features']:
for max_depth in param_grid['max_depth']:
    for min_samples_leaf in param_grid['min_samples_leaf']:
        for min_samples_split in param_grid['min_samples_split']:
            for n_estimators in param_grid['n_estimators']:

                gbr = GradientBoostingRegressor(loss=best_loss, learning_rate=best_learning_rate, 
                    n_estimators=n_estimators, criterion=best_criterion, min_samples_split=min_samples_split, 
                    min_samples_leaf=min_samples_leaf, max_depth=max_depth)

                gbr.fit(X_train, y_train)
                
                print('Done iteration: ', i)

                y_pred = gbr.predict(X_valid)
                mse = mean_squared_error(y_valid, y_pred)

                print('mse: ', mse)

                if mse < best_mse:
                    best_mse = mse
                    best_gbr = gbr
                i+=1

The mean squared error for the validation set goes down to 0.0593 after grid search optimization.

Lets apply the optimized gbr algorithm to the test set and see what the results look like.

The results look reasonably good. We get a pretty strong signal on Jul. 22 to sell the stock and we can see that 2 days later the stock drops precipitously. On the other hand, we also get a pretty strong signal to sell on May 14 and 15, but the price rises after May 15. So if we were holding stocks on those dates, it wouldn’t have been a great idea to sell.

Check out the notebook here

References:

  1. Dash, R., & Dash, P. K. (2016). A hybrid stock trading framework integrating technical analysis with machine learning techniques. The Journal of Finance and Data Science, 2(1), 42–57. https://doi.org/10.1016/j.jfds.2016.03.002
 stock charts  stock prices  stock indicators  gradient boosting  regression

Comments

Related Posts